|
Générateur pseudo-aléatoire
Dans le cadre d'une simulation, il est important d'avoir un bon générateur de nombres pseudo-aléatoires.
Cependant, il est tout aussi important de ne pas faire n'importe quoi avec. Il faut initialiser la
graine avec une valeur connue (reproductible), il ne faut pas utiliser un générateur pour en faire
plusieurs, ou ils seront corrélés... Bref, le cadre de travail est exigeant.
Ci-dessous se trouvent quelques mises en situation montrant grossièrement la validité de l'implémentation, à partir de plusieurs milliers de tirages comparés à la distribution réelle attendue. | ||
|
Téléchargement
Version Singleton
Version Autonome
| ||||||||||||||||||
|
Loi Uniforme
Nombre entier uniforme dans [|0;100|]
Random::Uniform<int>(0,100) ![Génération uniforme dans [|0;100|]](images/uniforme-int.png) Moyenne attendue :50, Moyenne observée: 50.0838, Ecartype observé: 29.0984
Nombre réel uniforme dans [0;1]
Random::Uniform<double>(0,1) ![Génération uniforme dans [0;1]](images/uniforme-double.png) Moyenne attendue: 0.5, Moyenne observée: 0.500823, Ecartype observé: 0.288113 | ||
|
Loi Gaussienne
Notez bien qu'il sagit de
Gaussienne(moyenne=1.234, ecartype=5.678) Random::Gaussian(1.234, 5.678) 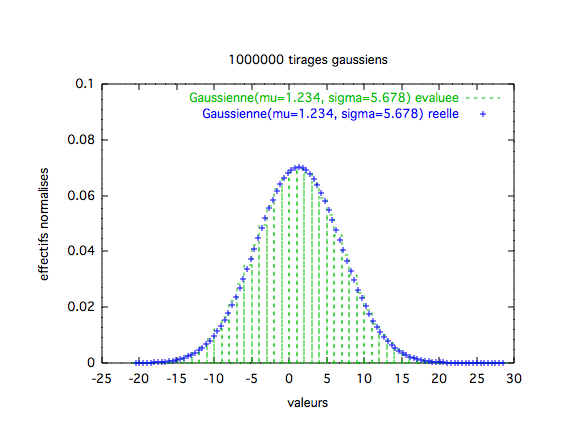 Moyenne observée: 1.23639, Ecartype observé: 5.67899 | ||
|
Loi Exponentielle
Exponentielle(lambda=2) Random::Exponential(lambda=2) 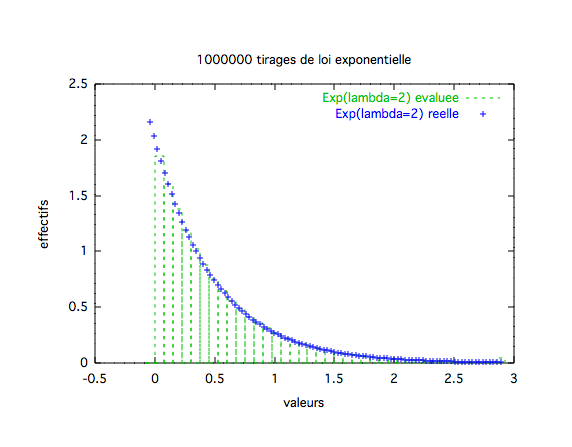 Moyenne observée:0.502966, Ecartype observé:0.511291 | ||
|
Performances
Les performances du générateur standard du C sont très variables selon les systèmes, la version du compilateur, comme le montrent les graphiques ci-après. Les tests effectués ne sont pas très pertinents, mais permettent de se faire une idée de l'impact sur les temps de calcul de l'utilisation du générateur que je vous fournis. Globalement, le générateur standard rand() est plus rapide, on pouvait s'y attendre. Mais avec des options d'optimisation, les performances du générateur que je vous fournis restent très honorables en comparaison, surtout vu le gain en propreté et en garanties. Les temps indicatifs donnés dans le graphique ci-dessous ont été calculés grâce à un programme effectuant 100 000 000 tirages avec un "(float)rand()/RAND_MAX", puis 100 000 000 tirages avec un "Random::Uniform()". Lancé plusieurs fois d'affilée, le programme avait des temps d'exécution stables, à moins d'une seconde près. 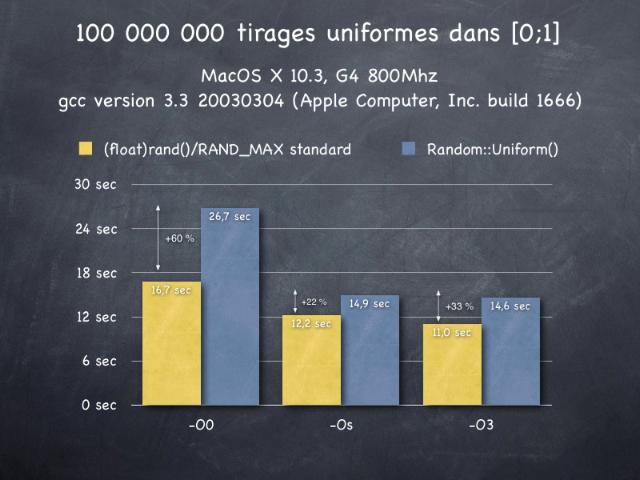 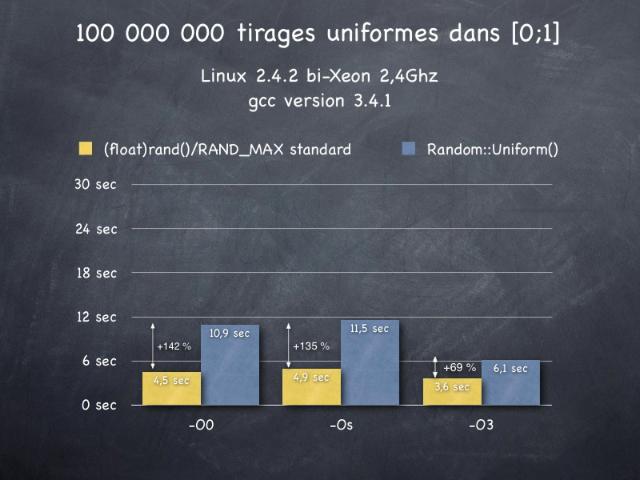 | ||