TestsÀ part la factorielle et la puissance, les fonctions que j'ai implémentées via leurs développements en séries entières prennent en paramètre l'ordre de développement à utiliser. Plus cet ordre est grand, plus les instanciations seront profondes, plus la compilation sera longue, mais plus les résultats seront précis. Il m'a semblé intéressant de relever l'ordre requis pour une précision donné pour savoir quelle valeur donner aux paramètres en fonction des besoins. Voici donc les résultats obtenus et commentés, tracés avec GNUPlot. J'y parle de précision relative et de précision absolue. Il s'agit simplement de l'évaluation de l'erreur relative et de l'erreur absolue. Notez enfin que lorsque les fonctions sont disponibles en version float et double, c'est la version double qui a servi au test. 
| ||
Précision à première vue :La convergence est extrêmement rapide. L'ordre 5 est déjà une bonne approximation (3.14157 au lieu de 3.14159). 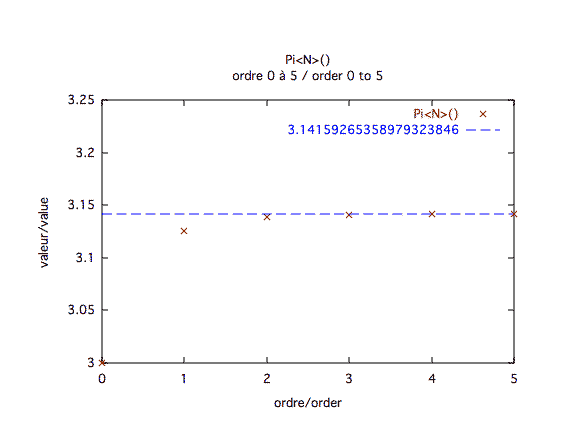
Précision obtenue selon l'ordre :L'ordre 5 est précis à 1e-4. La précision augmente quasi-linéairement avec l'ordre. À l'ordre 20, on atteint presque la limite de précision habituelle des double en C sur processeur 32 bits. (de l'ordre de 1e-17). 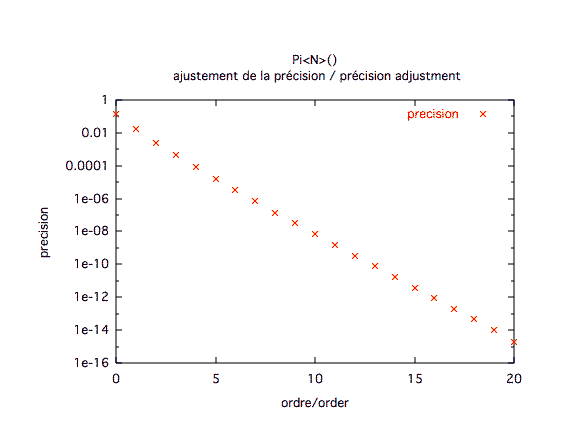
Ordre nécessaire pour une précision donnée :Voici le tableau inverse, l'ordre nécessaire à une précision donnée. 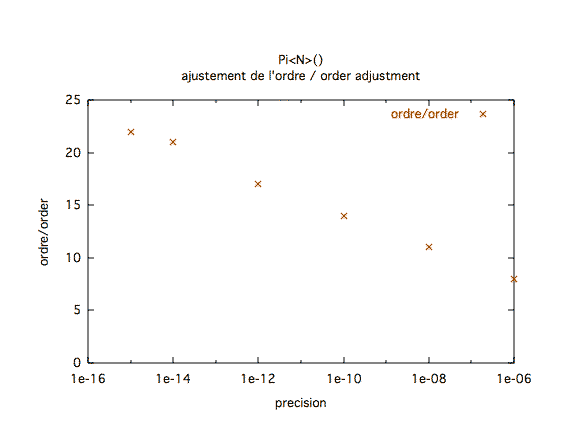
| ||
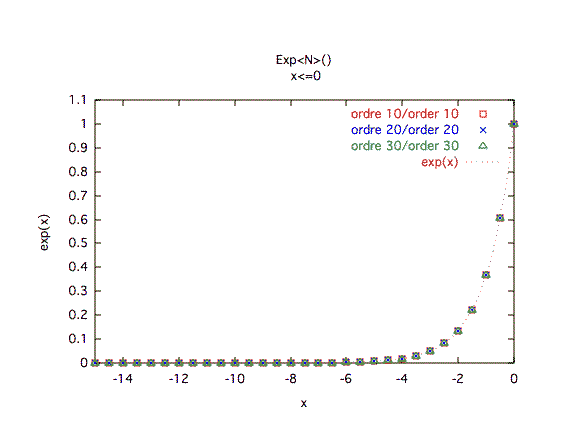
Précision à première vue :x ≥ 0 : comme prévu, un ordre faible n'est acceptable que pour les abcisses proches de 0. L'ordre 20 doit être suffisant en moyenne, mais on peut aller chercher l'ordre 30 pour les cas extrêmes. x ≤ 0 : la technique du exp(-x) = 1/exp(x) est vraiment efficace: elle écrase complètement l'imprécision, à tout ordre. 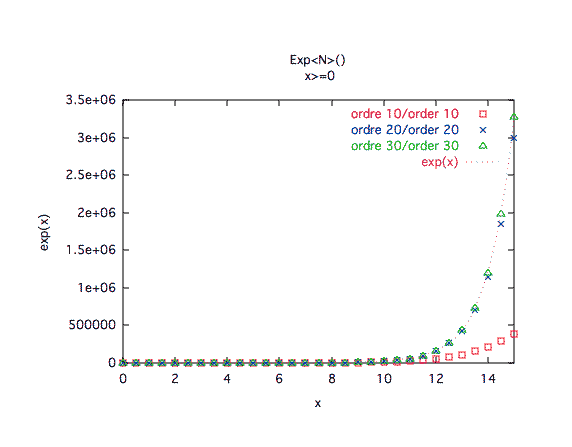
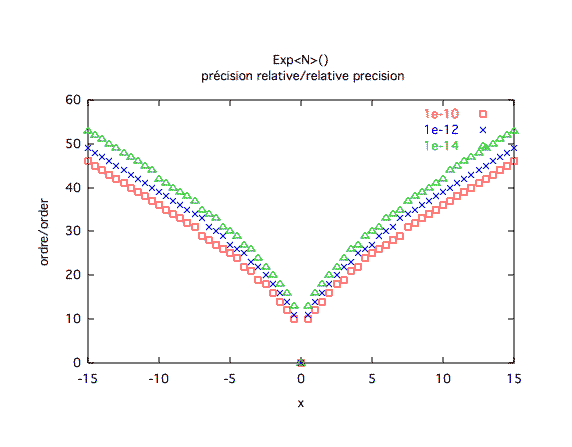
Précision relative :La précision relative est symétrique en x et quasi-linéaire. 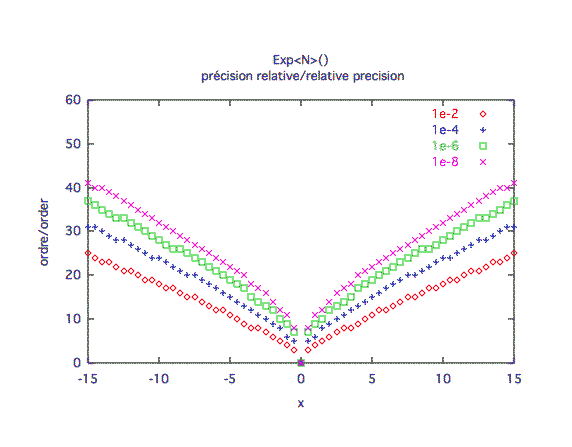
Précision absolue :Comme prévu, la précision absolue est moins gourmande pour les x négatifs. 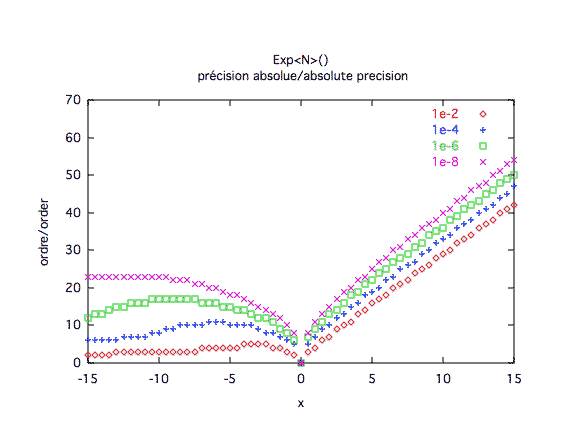
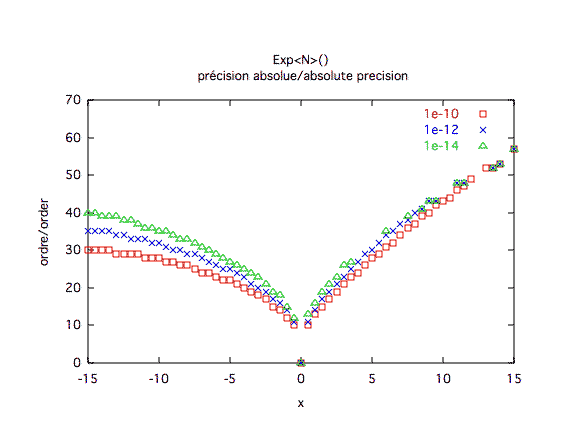
| ||
Précision à première vue :L'ordre 10 est insuffisant; l'ordre 20 semble suffisant sur [-2π ; 2π], mais les courbes de précision montrent qu'il vaut mieux monter à l'ordre 30. 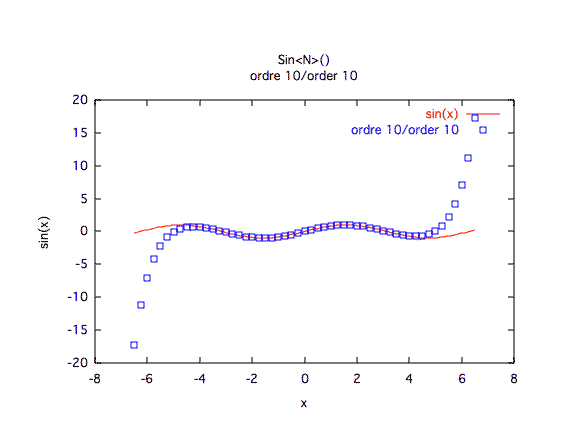
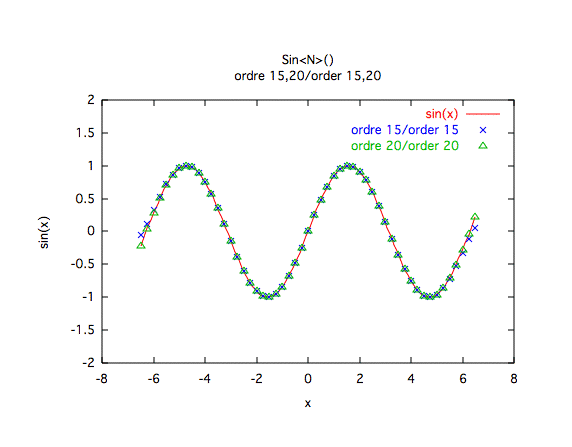
Précision relative :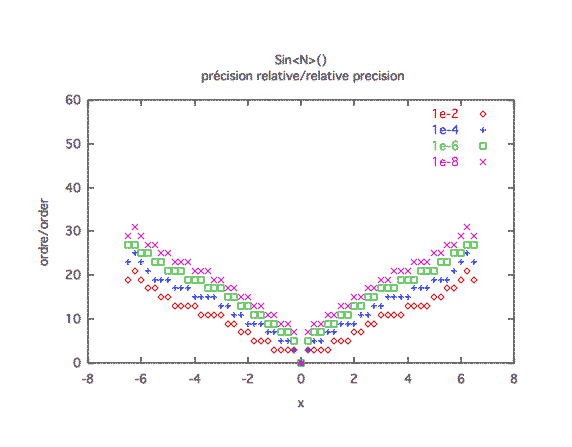
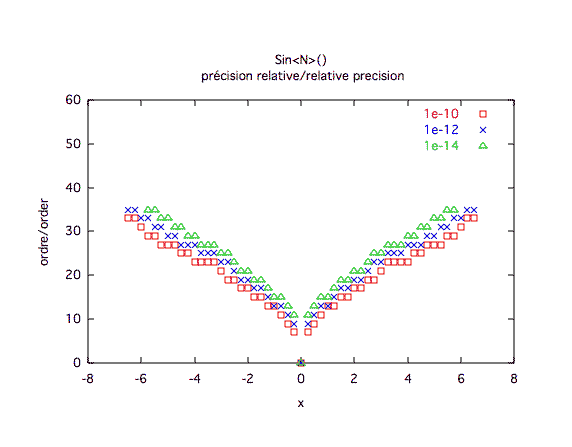
Précision absolue :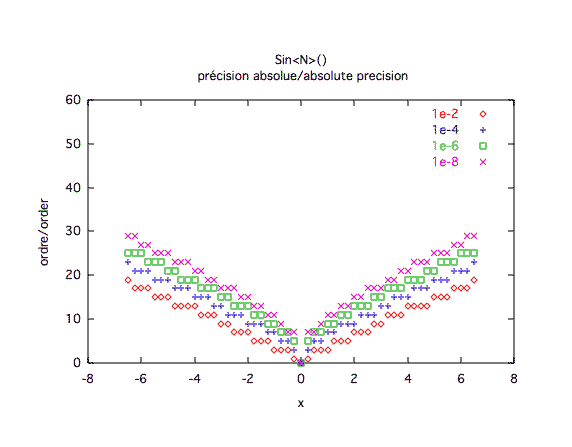
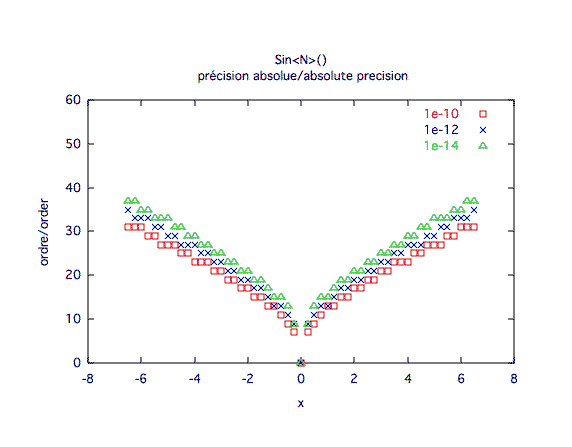
| ||
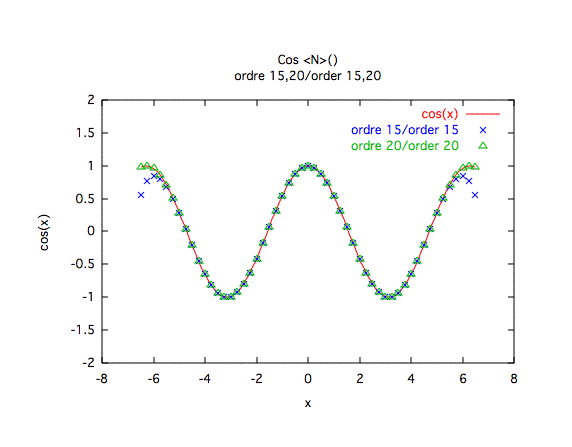
Précision à première vue :L'ordre 10 est insuffisant, il faut au moins un ordre 20 pour rester acceptable. 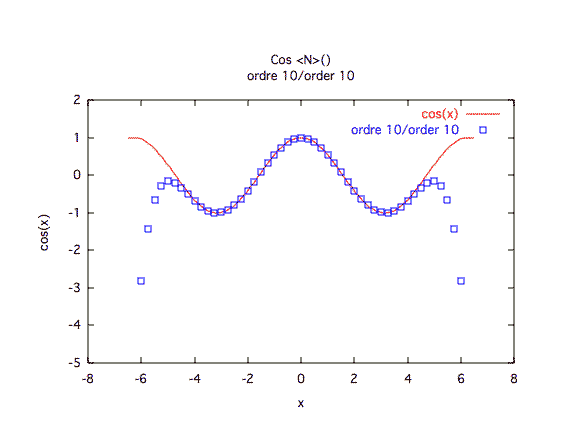
Précision relative :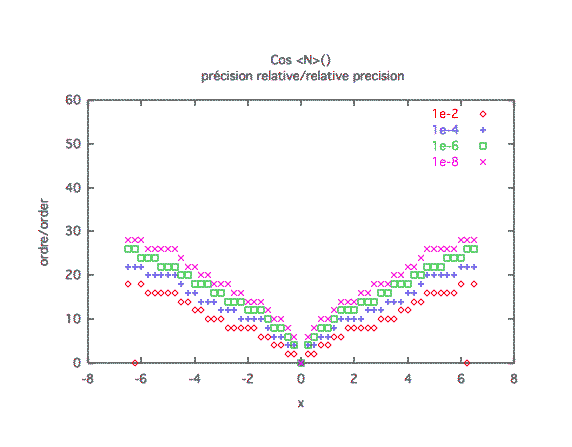
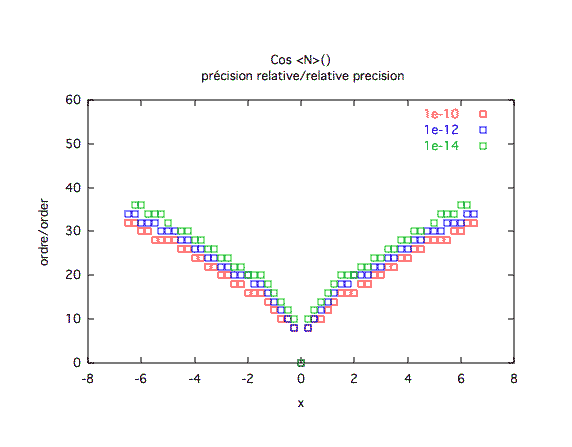
Précision absolue :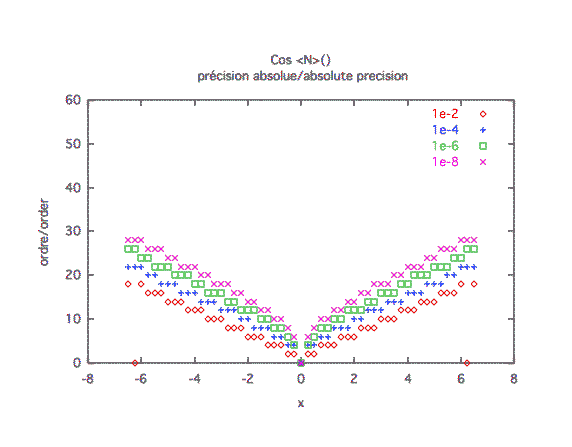
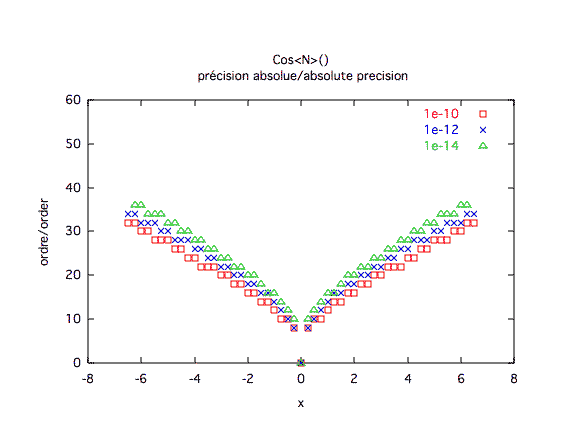
| ||
Précision à première vue :L'ordre 10 semble suffisant, mais les grands écarts de valeurs sont mal représentés ici. En fait, les courbes de précision font préférer l'ordre 30. 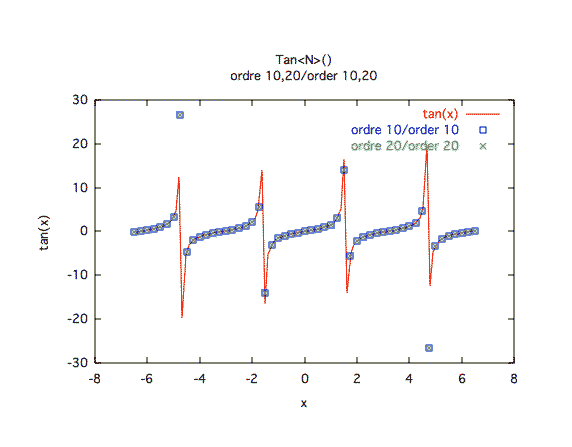
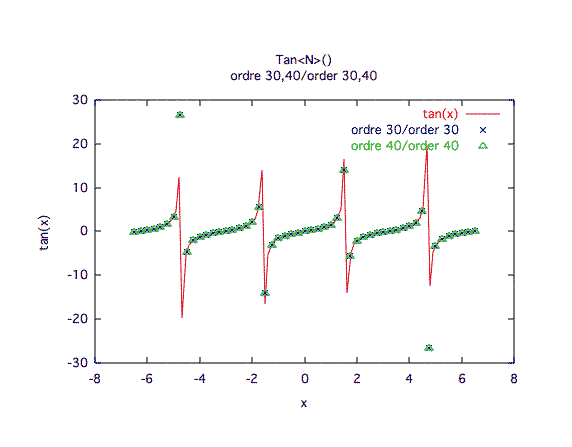
Précision relative :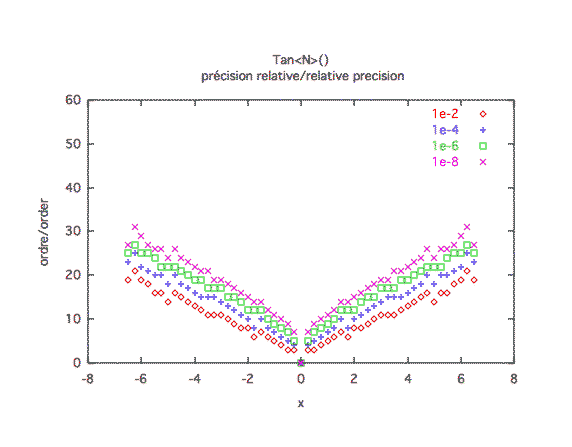
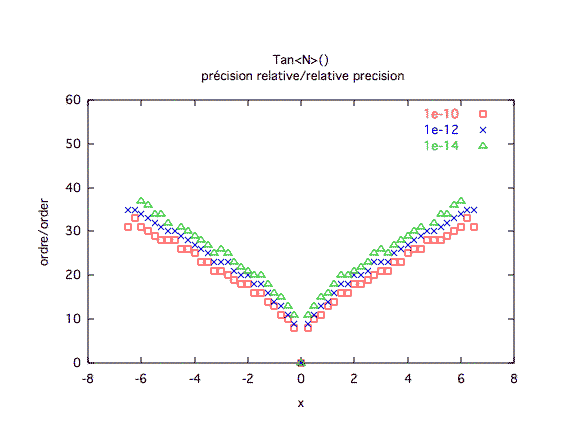
Précision absolue :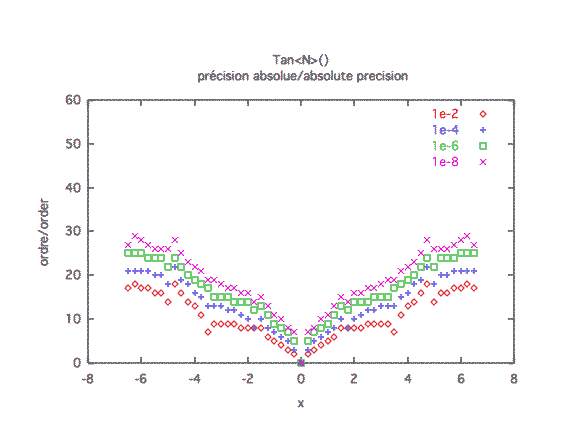
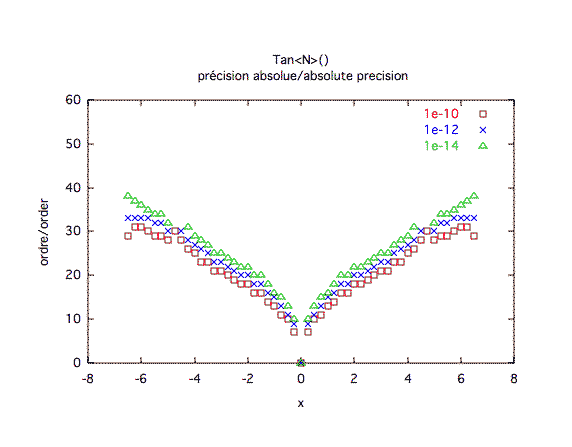
| ||
Précision à première vue :Dès que l'on s'approche de 1 ou -1, une bonne précision est difficile à obtenir. 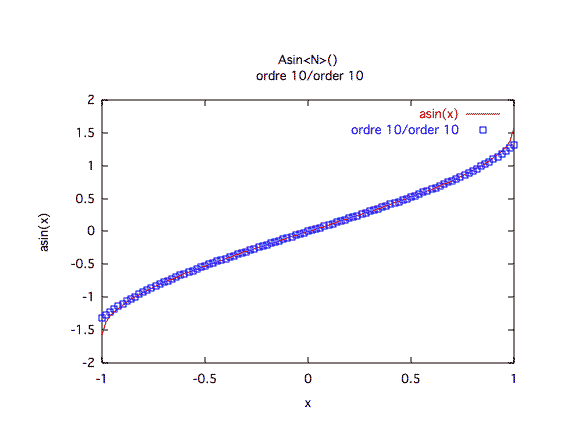
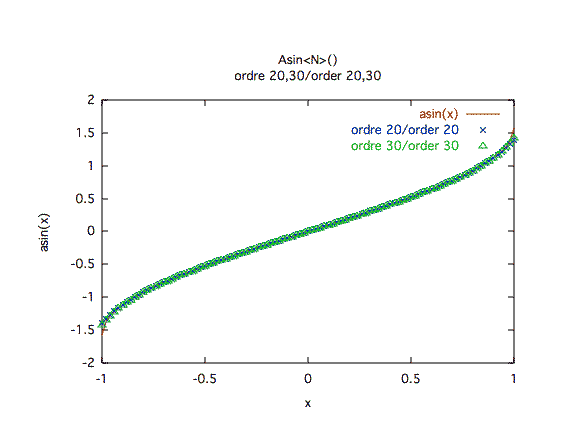
Précision relative :L'ordre 20 est suffisant sur une large plage de valeur, mais les bords sont problématiques. On constate un palier sur les bords de la courbe, mais ici, l'algorithme a en fait échoué en produisant NaN (Not a Number). 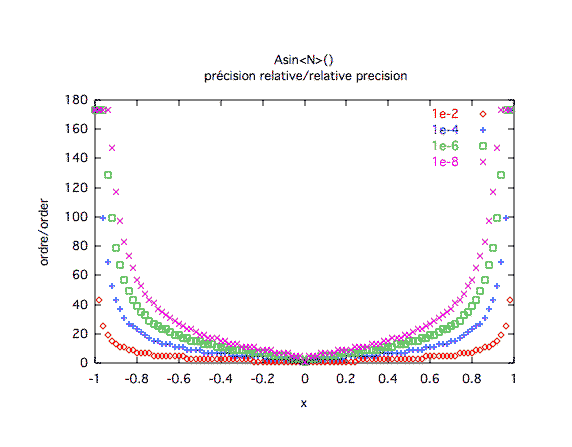
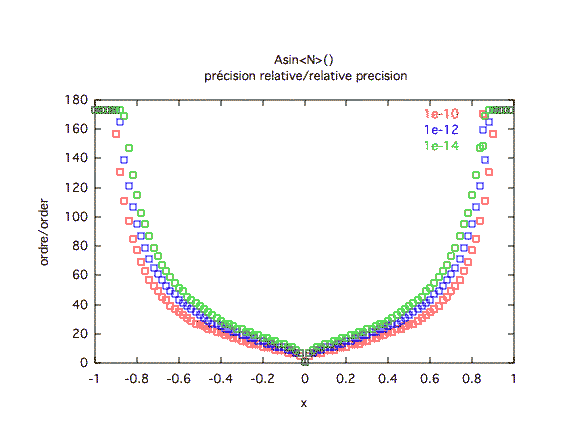
Précision absolue :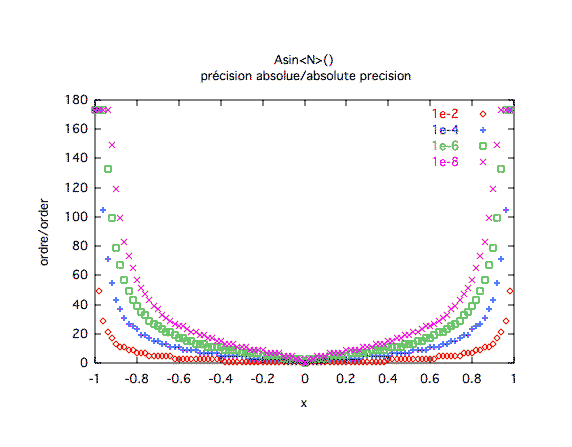
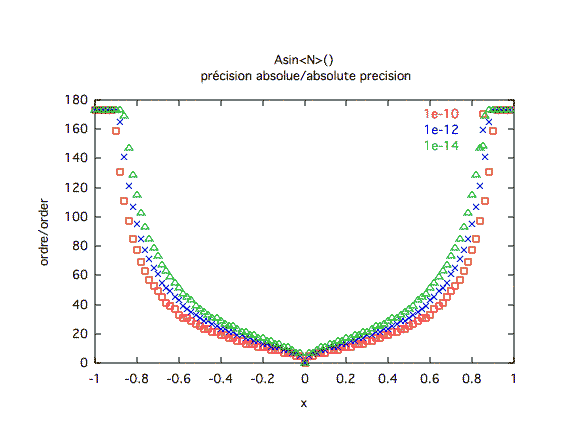
| ||
Précision à première vue :Dès que l'on s'approche de 1 ou -1, une bonne précision est difficile à obtenir. 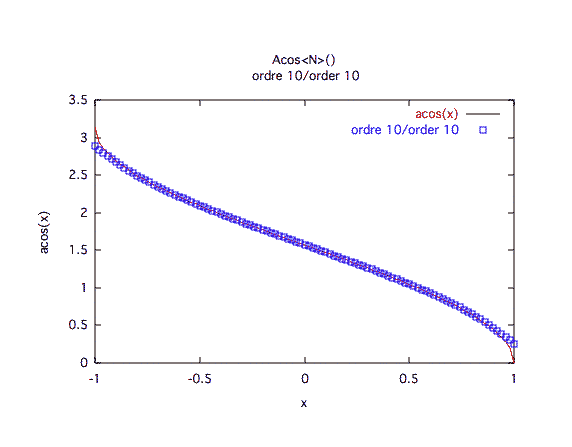
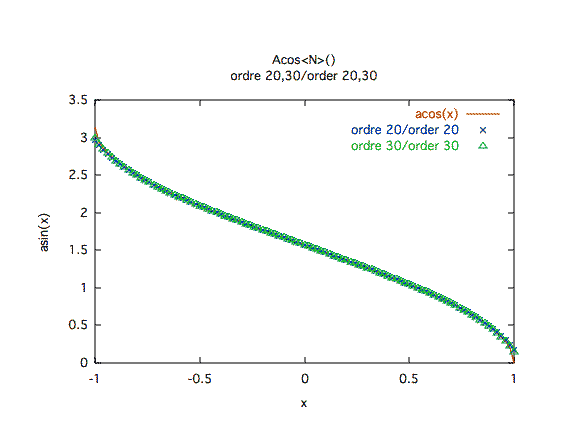
Précision relativeL'ordre 20 est suffisant sur une large plage de valeur, mais les bords sont problématiques. On constate un palier sur les bords de la courbe, mais ici, l'algorithme a en fait échoué en produisant NaN (Not a Number). 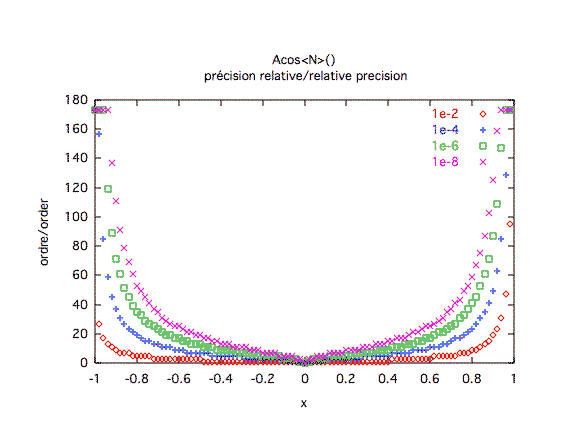
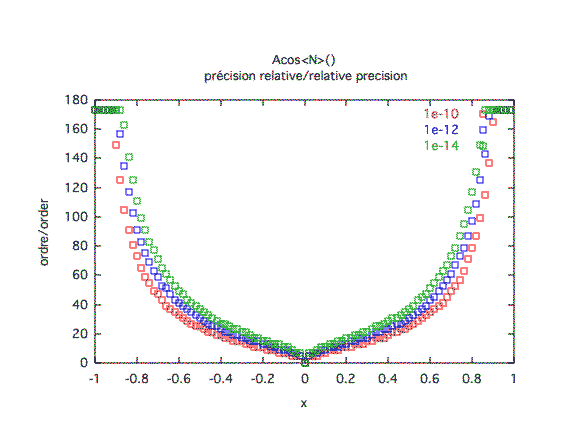
| ||
Précision à première vue :L'ordre 10 est très performant. Voyez cependant les courbes de précision qui dévoilent une subtilité. 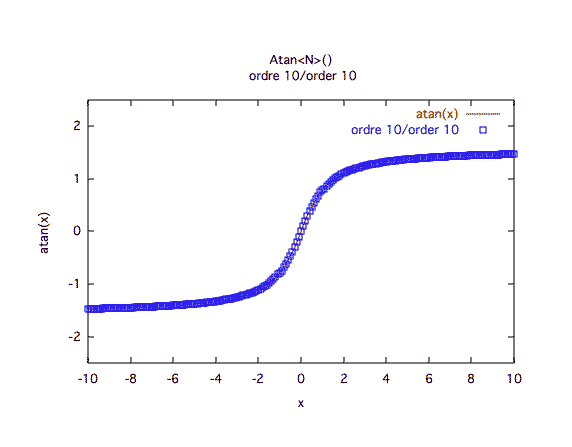
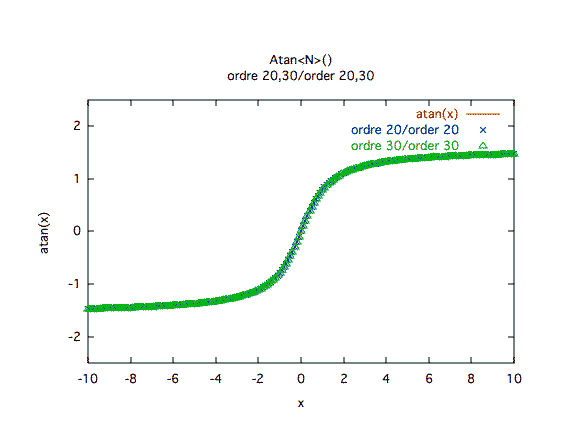
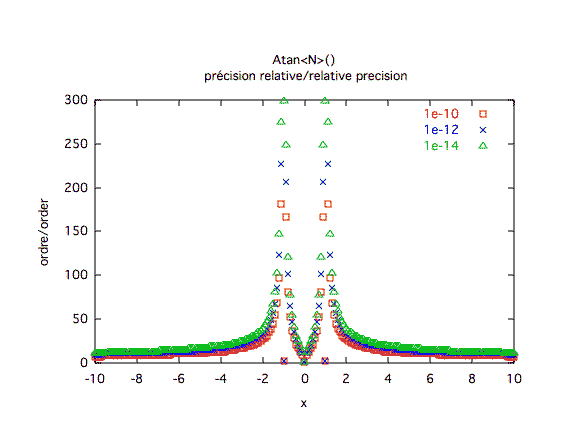
Précision relative :Le problème de convergence en 1 et -1 est assez évident. Il n'apparaît pas sur les courbes précédentes grâce à l'astuce d'imposer la valeur +/-π/4 quand on s'approche très près de 1 ou -1. 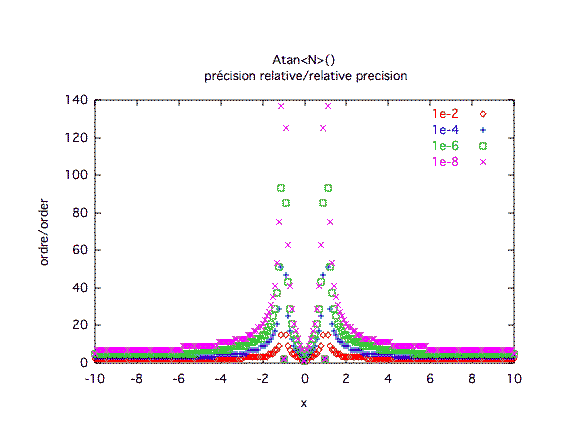
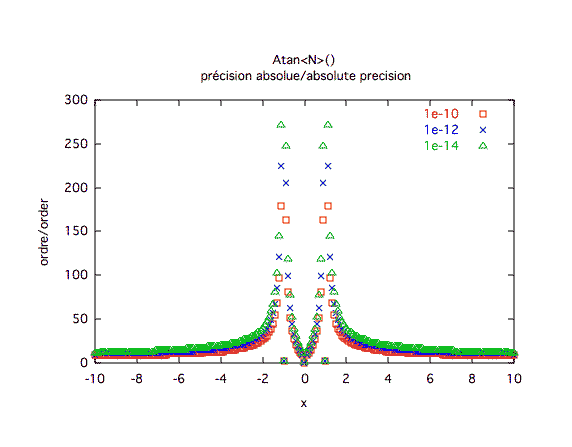
Précision absolue :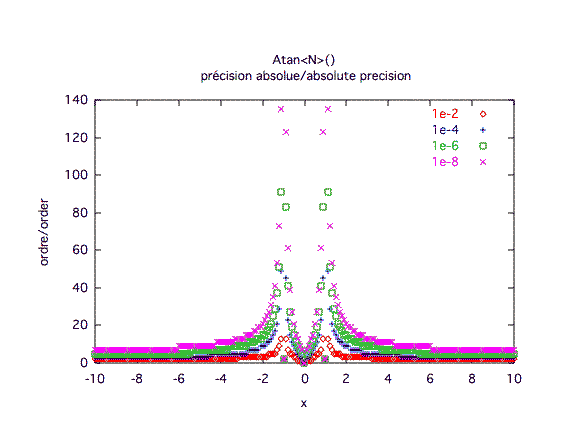
| ||
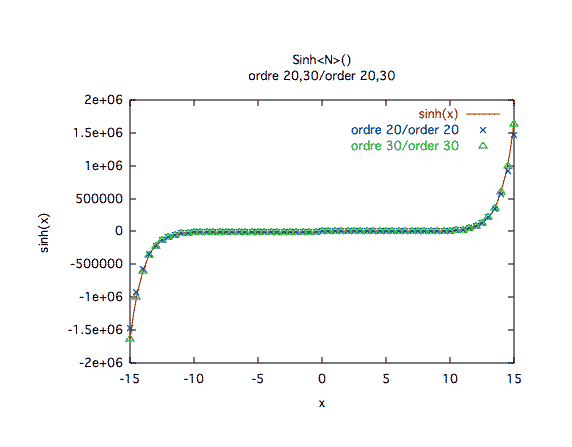
Précision à première vue :L'ordre 10 est clairement insuffisant, l'ordre 30 est plus sage dès qu'on est loin de 0. 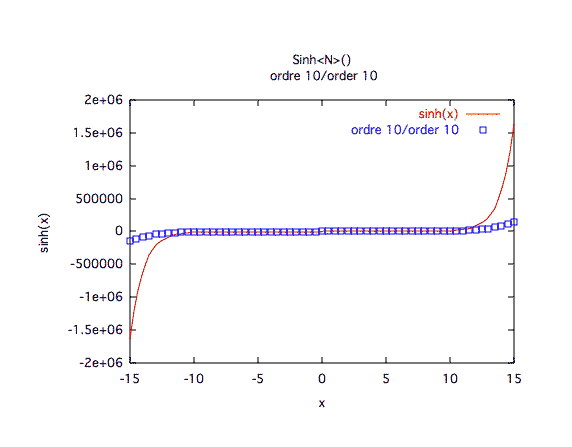
Précision relative :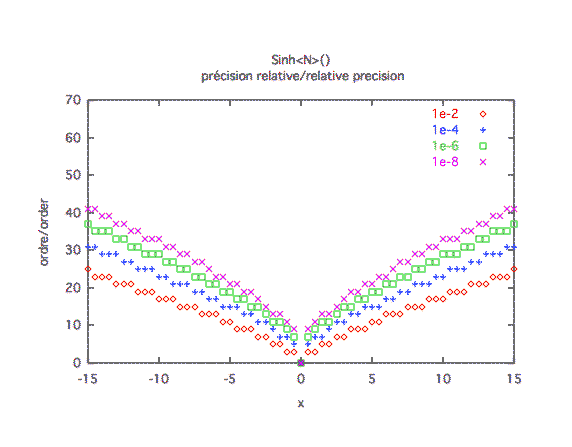
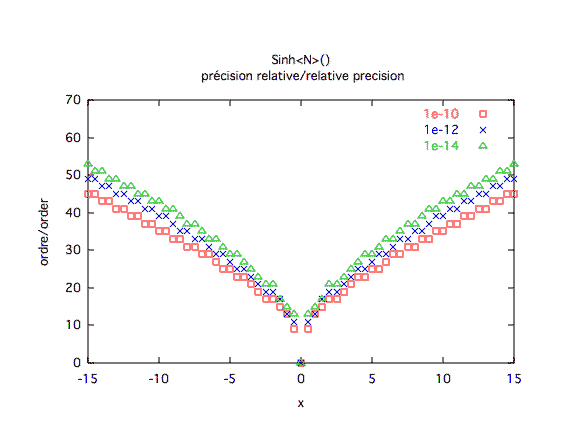
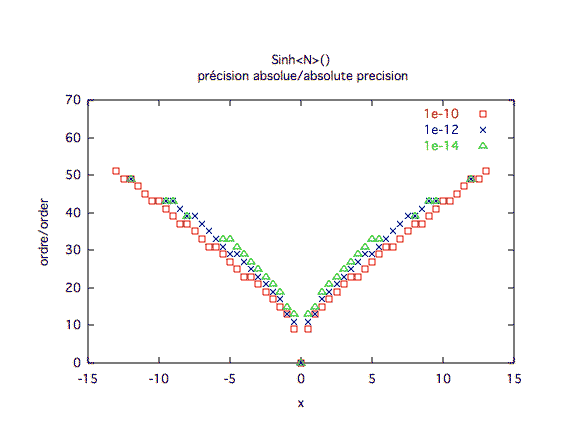
Précision absolue :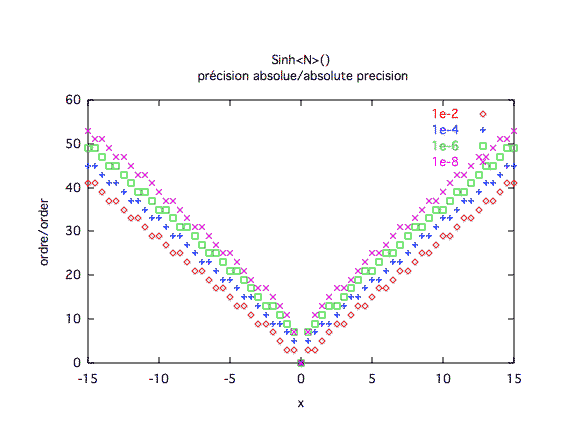
| ||
Précision à première vue :L'ordre 10 est clairement insuffisant, l'ordre 30 est plus sage dès qu'on est loin de 0. 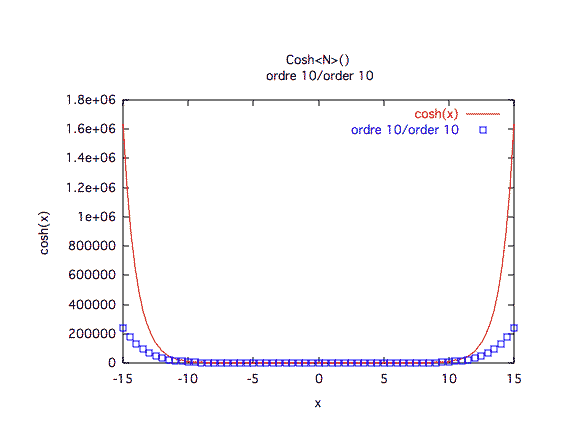
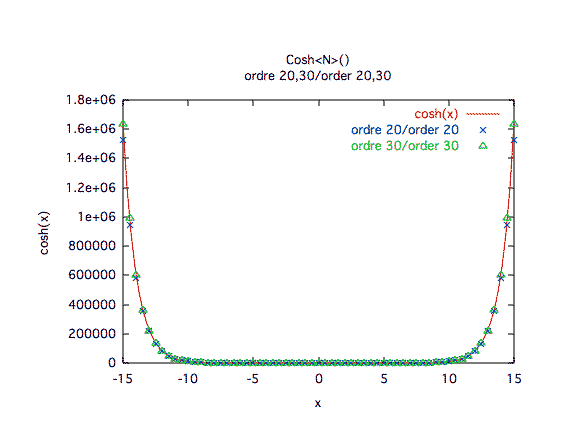
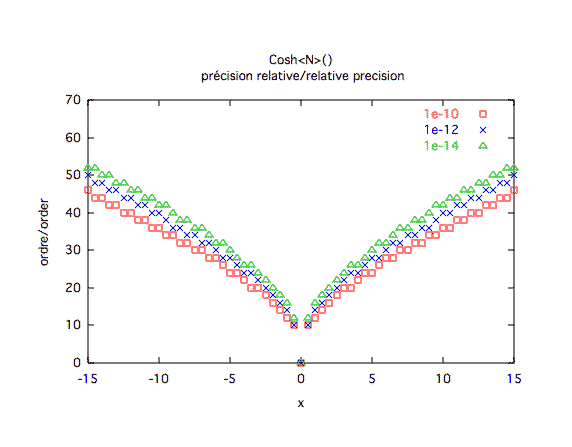
Précision relative :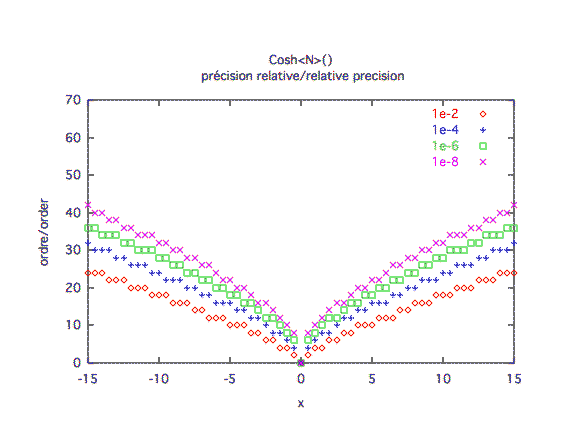
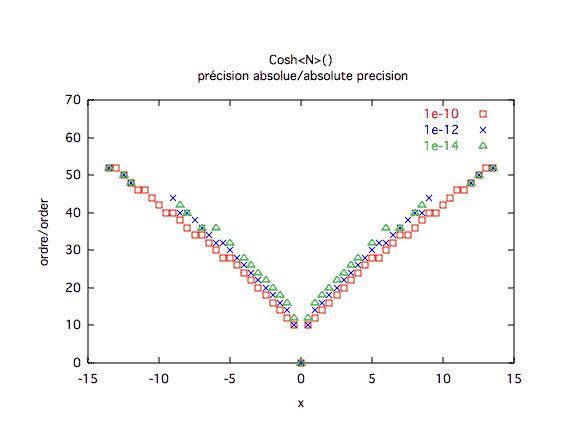
Précision absolue :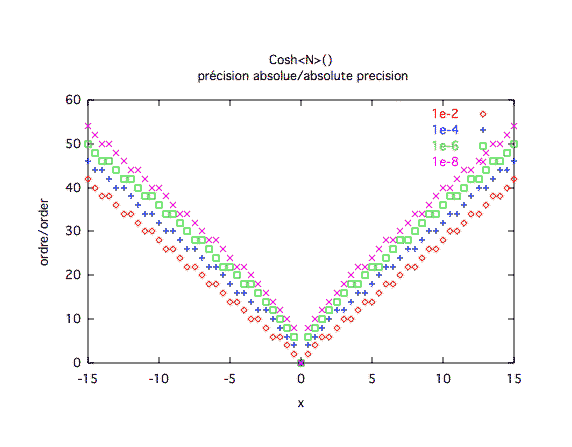
| ||
Précision à première vue :L'ordre 10 est clairement insuffisant, l'ordre 20 est une bonne approche. 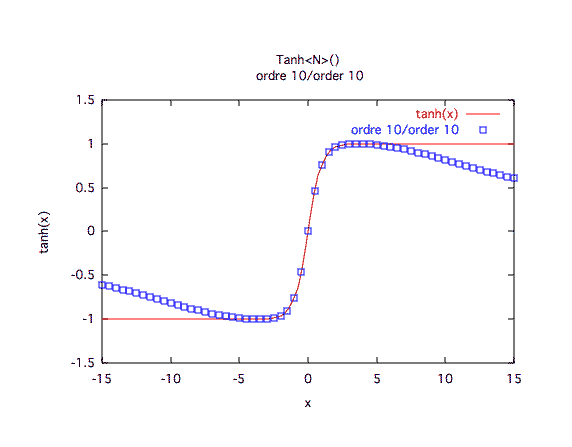

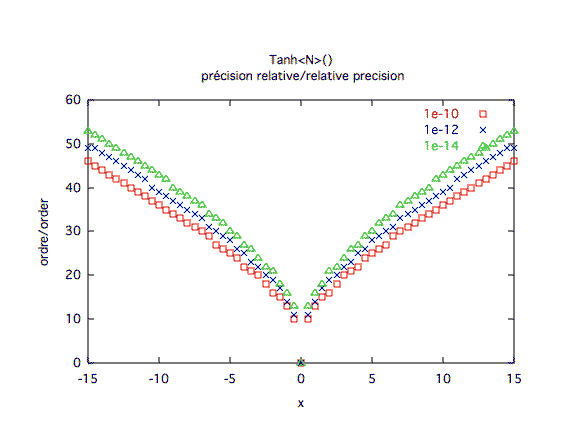
Précision relative :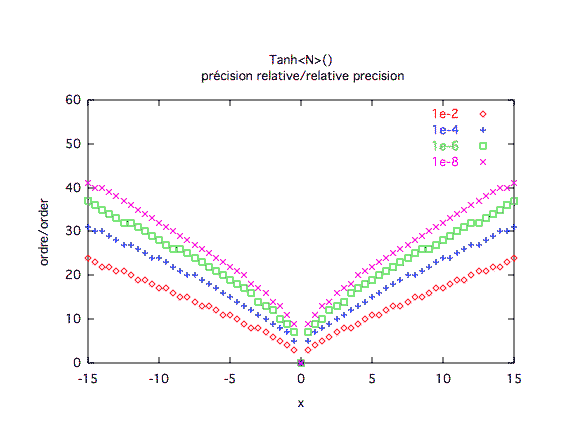
Précision absolue :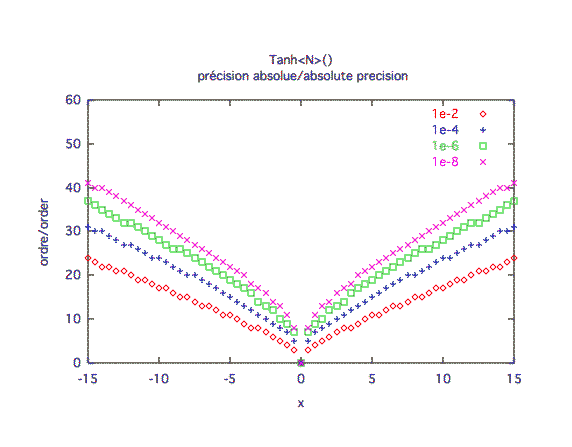
| ||
Précision à première vue :L'ordre 10 est clairement insuffisant, l'ordre 30 est une bonne approche. 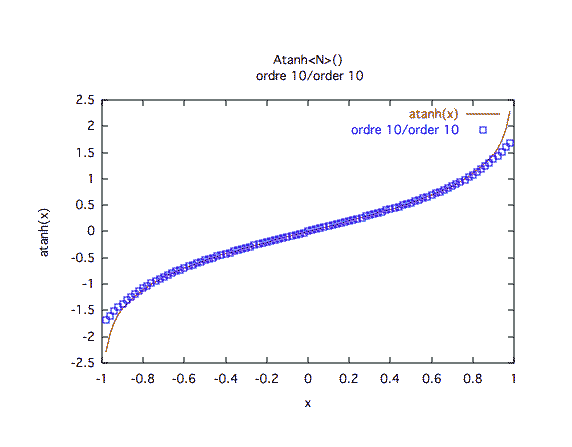
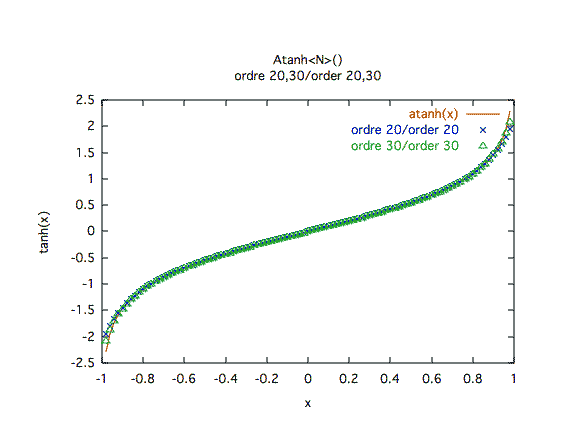
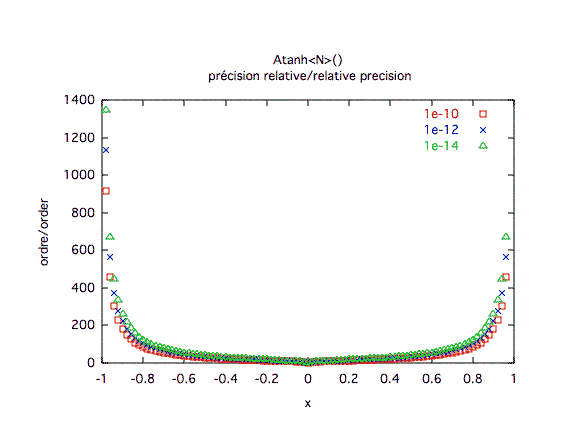
Précision relative :La convergence est réellement mauvaise sur les bords. 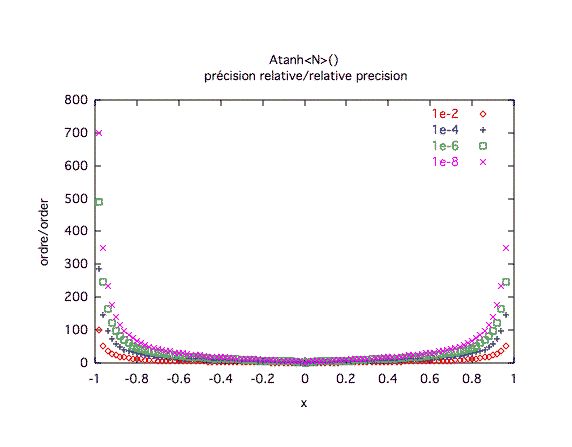
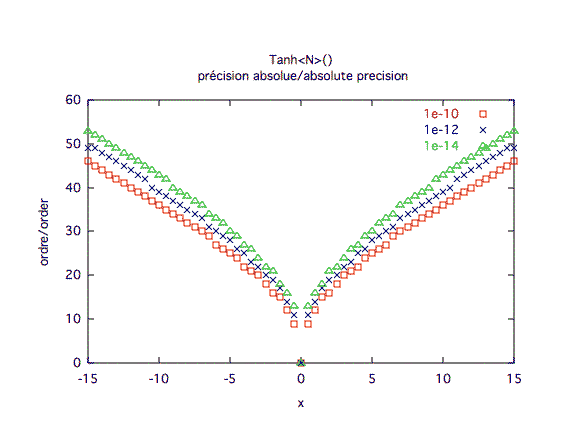
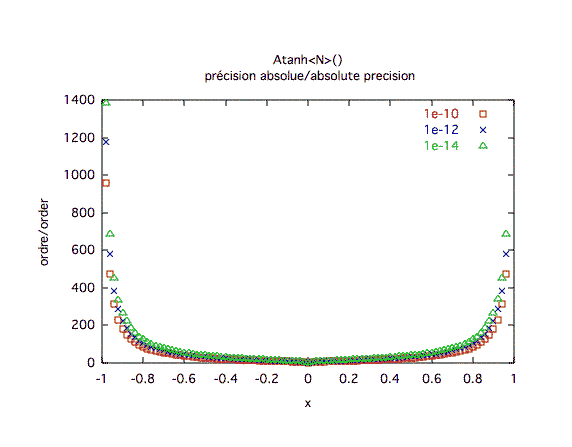
Précision absolue :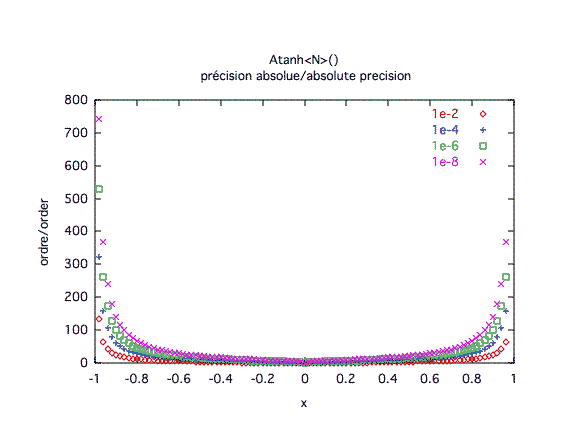
| ||