|
Une classe Matrix, pour quoi faire?
Il est pénible en C ou en C++ d'allouer et désallouer proprement un tableau bi-dimensionnel.
Il est également long d'implémenter correctement des fonctions comme le redimensionnement, le décalage d'éléments...
Pour mes besoins, j'ai créé une classe Matrix disposant d'assez de méthodes pour un usage extrêmement
général. Ses caractéristiques sont les suivantes:
| ||
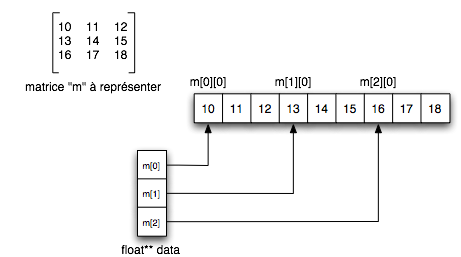
L'inconvénient est que les très grandes matrices ne pourront pas être allouées. Mais pour des travaux sur de telles matrices, MathLab ou ses équivalents gratuits sont sans doute plus adaptés. En revanche, les avantages sont multiples:
| ||
|
J'ai séparé le code en deux fichiers : Matrix.hxx ressemble à un fichier d'en-tête standard :
il regroupe les déclarations de la classe et des méthodes. Le code correspondant a été déporté dans
Matrix.h, qui inclut Matrix.hxx. Pour les optimisations Altivec se trouvent également
deux fichiers : Altivec.h et Altivec.cpp. Ils ne sont pas nécessaires si vous ne comptez
pas bénéficier de l'Altivec. Voyez la partie Instructions de compilation pour
savoir quels fichiers inclure et comment compiler le code.
| ||||||||||||
| ||
|
template <typename T>
Matrix(unsigned int height=0, unsigned int width=0,
const T& fill=T(),bool binarymode = true)
Construit une matrice de taille donnée height*width, et la remplit avec l'objet fill
(Appel au constructeur par défaut du type T; cela donne 0 pour les types de base).
On peut également spécifier à ce niveau via binarymode si la matrice doit
utiliser les traitements binaires sur les éléments. (VRAI par défaut).
Matrix(const Matrix<U> other)
Recopie la matrice other, qui peut être d'un autre type. Matrix(const Matrix<U> other,unsigned int fromRow, unsigned int fromCol) Recopie la matrice other, qui peut être d'un autre type, en commençant aux coordonnées [fromRow][fromCol]. Si ces coordonnées débordent de la matrice source, la matrice créée est vide. Exemple :
Matrix(const Matrix<U> other,unsigned int fromRow, unsigned int fromCol, unsigned int height, unsigned int width, const T& fill = T(), bool loop = false) Recopie la matrice other, qui peut être d'un autre type, en commençant aux coordonnées [fromRow][fromCol], et uniquement sur une hauteur height et une largeur width. Si les valeurs provoquent un débordement de la matrice initiale, l'espace vide de la matrice destination est rempli avec fill. Si loop est VRAI, l'espace est rempli en bouclant sur la matrice source. Exemples :
unsigned int height Hauteur de la matrice (nombre de lignes). Implémentée comme unsigned int pour être toujours positive. Si height OU width est nul, la matrice ne contient aucune donnée, le tableau contenant les adresses des n lignes est alors de taille 0. height est accessible via getHeight() et modifiable via resize(). unsigned int width Largeur de la matrice (nombre de colonnes). Implémentée comme unsigned int pour être toujours positive. Si height OU width est nul, la matrice ne contient aucune donnée, le tableau contenant les adresses des n lignes est alors de taille 0. width est accessible via getWidth) et modifiable via resize(). bool binarymode Si binarymode est VRAI, l'implémentation s'autorise l'utilisation de memcpy() et memmove(). Cela est très déconsillé si le type T de la matrice est une classe dont les instances encapsulent des ressources. binarymode est accessible via getBinaryMode() et modifiable via setBinaryMode(). bool getHeight(void) const Renvoie la hauteur height de la matrice. bool getWidth(void) const Renvoie la largeur width de la matrice. T** getData(void) const Renvoie le tableau contenant les adresses des lignes. Pour une matrice M, M[i][j] est équivalent à M.getData()[i][j] (où 0≤i≤height et 0≤j≤width). getData()[0] est l'adresse de début du tableau unidimensionnel contenant les éléments. Voyez la partie Implémentation et performance pour plus de détails. getData() renvoie 0 si la matrice est vide, i.e. height ou width vaut 0. bool getBinaryMode(void) const Renvoie l'état de binarymode Matrix<T>& resize(unsigned int newHeight,unsigned int newWidth, const T& fill = T()) Redimensionne la matrice à partir de son coin supérieur gauche. Si la nouvelle taille fait apparaître de nouveaux éléments, ceux-ci sont initialisés à fill (0 par défaut pour les types de base). La fonction renvoie la matrice modifiée. Exemple:
Matrix<T>& resize(unsigned int newHeight, unsigned int newWidth, unsigned int topMargin, unsigned int leftMargin,const T& fill = T()) Redimensionne la matrice à partir de son coin supérieur gauche en laissant la marge spécifiée en haut (topMargin) et à gauche (leftMargin). Si la nouvelle taille fait apparaître de nouveaux éléments, ceux-ci sont initialisés à fill (0 par défaut pour les types de base). La fonction renvoie la matrice modifiée. Exemple:
void setBinaryMode(bool mode) const Modifie l'état de binarymode Opérateurs membresoperator=(const Matrix<U> other)Recopie la matrice other, qui peut être d'un autre type. T* operator[](unsigned int row) Accède à la ligne row. On peut alors chaîner avec un autre [] pour accéder à une case de cette ligne. Remarques:
const T* operator[](unsigned int row) const Cette fonction se comporte comme la version non-const; mais c'est une surcharge nécessaire pour la lecture seule d'une case dans un contexte const. Matrix<T>& operator+=(const Matrix<U>& other) Ajoute à la matrice le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator-=(const Matrix<U>& other) Soustrait à la matrice le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator*=(const Matrix<U>& other) multiplie (case par case) la matrice par le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Remarque : je ne fournis pas d'opération de calcul matriciel. Si vous voulez effectuer une véritable multiplication matricielle, il vous faut utiliser une librairie adptée, sui qaura vous en fournir une version optimisée. Exemple:
Matrix<T>& operator/=(const Matrix<U>& other) Divise (case par case) la matrice par le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator&=(const Matrix<U>& other) Effectue un ET binaire entre la matrice et le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator|=(const Matrix<U>& other) Effectue un OU binaire entre la matrice et le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator^=(const Matrix<U>& other) Effectue un OU EXCLUSIF binaire entre la matrice et le contenu d'une autre matrice. Si les matrices n'ont pas la même taille, l'opération est faite sur toutes les cases possibles à partir de [0][0]. Exemple:
Matrix<T>& operator+=(const U& x) Ajoute x a tous les élements de la matrice. Matrix<T>& operator-=(const U& x) Soustrait x a tous les élements de la matrice. Matrix<T>& operator*=(const U& x) multiplie par x tous les élements de la matrice. Matrix<T>& operator/=(const U& x) Divise par x tous les élements de la matrice. Matrix<T>& operator&=(const U& x) Effectue un ET binaire avec x pout tous les élements de la matrice. Matrix<T>& operator|=(const U& x) Effectue un OU binaire avec x pout tous les élements de la matrice. Matrix<T>& operator^=(const U& x) Effectue un OU EXCLUSIF binaire avec x pout tous les élements de la matrice. Matrix<T>& operator~(void) Effectue le complément à 1 de la matrice. Cette méthode est spécialement surchargée pour les matrices de type <bool>, où dans ce cas true devient false et vice-versa. Matrix<T>& operator++(void) Operateur de pré-incrémentation (ajoute 1 et renvoie la matrice modifiée). Matrix<T>& operator++(int) Operateur de post-incrémentation (ajoute 1 et renvoie la matrice dans son état antérieur). Matrix<T>& operator--(void) Operateur de pré-décrémentation (soustrait 1 et renvoie la matrice modifiée). Matrix<T>& operator--(int) Operateur de post-décrémentation (soustrait 1 et renvoie la matrice dans son état antérieur). Matrix<T> operator-(void) const Operateur "-" unaire. Renvoie la matrice dont chaque valeur a été changée en son opposée. Matrix<T>& operator()(U (*f)(V)) Applique la fonction f (de prototype U f(V)) à tous les éléments de la matrice. Exemple: M( static_cast<(double) (*)(double)>( std::cos ) ) applique le cosinus de la librairie standard à toute la matrice. Matrix<T>& operator()(U (*f)(const V&)) Cette méthode se comporte comme la précédente. C'est une surcharge pour certains cas d'utilisation. Matrix<T>& operator()(const U&) Applique un foncteur de classe U à tous les éléments de la matrice (Rappel : un foncteur est un objet bénéficiant d'un operator()). Opérateurs non membresostream& operator<<(ostream&)Affiche la matrice sur le flux, de façon lisible. Pour une opération de sauvegarde, il faut plutôt utiliser writeToStream(). istream& operator>>(istream&) Lit une matrice depuis un flux d'entrée. Cette opération est équivalente à readFromStream(). Le flux doit contenir la description d'une matrice telle qu'en produit writeToStream(). Matrix<T> operator+(const Matrix<T>& m1, const Matrix<T>& m2) Additionne deux matrices et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator+=). Matrix<T> operator-(const Matrix<T>& m1, const Matrix<T>& m2) Soustrait deux matrices et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator-=). Matrix<T> operator*(const Matrix<T>& m1, const Matrix<T>& m2) multiplie deux matrices élément par élément (ce n'est pas une multiplication matricielle au sens de l'algèbre linéaire), et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator*=). Matrix<T> operator/(const Matrix<T>& m1, const Matrix<T>& m2) Divise deux matrices élément par élément, et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator/=). Matrix<T> operator&(const Matrix<T>& m1, const Matrix<T>& m2) Effectue un ET binaire entre les deux matrices, élément par élément, et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator&=). Matrix<T> operator|(const Matrix<T>& m1, const Matrix<T>& m2) Effectue un OU binaire entre les deux matrices, élément par élément, et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator|=). Matrix<T> operator^(const Matrix<T>& m1, const Matrix<T>& m2) Effectue un OU EXCLUSIF binaire entre les deux matrices, élément par élément, et renvoie le résultat. Si les matrices n'ont pas la même taille, seule leur partie commune depuis [0][0] est concernée (voir operator^=). Matrix<T> operator+(const Matrix<T>& m1, const U& x) Matrix<T> operator+(const U& x, const Matrix<T>& m1) Ajoute x à tous les éléments d'une matrice. Matrix<T> operator-(const Matrix<T>& m1, const U& x) Matrix<T> operator-(const U& x, const Matrix<T>& m1) Soustrait x à tous les éléments d'une matrice. Matrix<T> operator*(const Matrix<T>& m1, const U& x) Matrix<T> operator*(const U& x, const Matrix<T>& m1) multiplie par x tous les éléments d'une matrice. Matrix<T> operator/(const Matrix<T>& m1, const U& x) Matrix<T> operator/(const U& x, const Matrix<T>& m1) Divise par x tous les éléments d'une matrice. Matrix<T> operator&(const Matrix<T>& m1, const U& x) Matrix<T> operator&(const U& x, const Matrix<T>& m1) Effectue un ET binaire entre x et tous les éléments d'une matrice. Matrix<T> operator|(const Matrix<T>& m1, const U& x) Matrix<T> operator|(const U& x, const Matrix<T>& m1) Effectue un OU binaire entre x et tous les éléments d'une matrice. Matrix<T> operator^(const Matrix<T>& m1, const U& x) Matrix<T> operator^(const U& x, const Matrix<T>& m1) Effectue un OU EXCLUSIF binaire entre x et tous les éléments d'une matrice. bool operator==(const Matrix<T>& m1, const Matrix<T>& m2) Teste si deux matrices sont égales (même taille et mêmes éléments). bool operator!=(const Matrix<T>& m1, const Matrix<T>& m2) Teste si deux matrices sont différentes (non égales). bool operator<(const Matrix<T>& m1, const Matrix<T>& m2) Teste si m1 est "strictement inférieure" à m2. L'algorithme est le suivant:
bool operator<=(const Matrix<T>& m1, const Matrix<T>& m2) Teste si m1 est "inférieure ou égale" à m2. L'algorithme est le suivant:
bool operator>(const Matrix<T>& m1, const Matrix<T>& m2) Teste si m1 est "strictement supérieure" à m2. L'algorithme est le suivant:
bool operator>=(const Matrix<T>& m1, const Matrix<T>& m2) Teste si m1 est "supérieure ou égale" à m2. L'algorithme est le suivant:
Méthodes membresMatrix<T>& transpose(void)transpose la matrice.
Matrix<T> subMatrix(unsigned int fromRow, unsigned int fromCol, bool loop = false) Extrait la sous matrice commençant à [fromRow][fromCol]. Si ces coordonnées sont extérieures à la matrice source, la matrice résultante dépend de loop. Si loop est FAUX, elle sera vide, si loop est VRAI, fromRow et fromCol sont réinterprétés modulo height et width.
Matrix<T> subMatrix(unsigned int fromRow, unsigned int fromCol, unsigned int height, unsigned int width, const T& fill = T(), bool loop=false) Extrait la sous-matrice commençant aux coordonnées [fromRow][fromCol], et de taille height*width. S'il y a débordement de la matrice source, l'espace vide est comblé par fill (0 par défaut pour les types de base), ou bien, si loop est VRAI, par les données de la matrice source dont on considère qu'elle boucle.
Matrix<T>& reset(const T& fill = T()) Remplit la matrice avec fill (0 par défaut pour les types de base). Matrix<T>& fillWith(const T& fill) Remplit la matrice avec fill. Matrix<T>& fillWith(const Matrix<U>& other, bool loop = false) Remplit la matrice (à partir de [0][0]) avec les données de la matrice other, depuis les coordonnées [0][0]. Si cette matrice est plus petite, et que loop est FAUX, le reste de la matrice destination est laissé intact; si loop est VRAI, toute la matrice destination est remplie en répétant la matrice other autant de fois que nécessaire. Matrix<T>& fillWith(const Matrix<U>& other, unsigned int fromRow, unsigned int fromCol, bool loop = false) Remplit la matrice (à partir de [0][0]) avec les données de la matrice other, depuis les coordonnées [fromRow][fromCol]. Si cette matrice est plus petite, et que loop est FAUX, le reste de la matrice destination est laissé intact; si loop est VRAI, fromRow et fromCol sont réinterprétés modulo height et width, et toute la matrice destination est remplie en répétant la matrice other autant de fois que nécessaire. Matrix<T>& fillWith(const Matrix<U>& other, unsigned int fromRow, unsigned int fromCol, unsigned int height, unsigned int width, bool loop = false) Remplit la matrice (à partir de [0][0]) avec les données de la matrice other, depuis les coordonnées [fromRow][fromCol], et sur les longueurs height et width. Si la taille précisée fait sortir de la matrice et que loop est FAUX, seule la partie valide est concernée; si loop est VRAI, fromRow et fromCol sont réinterprétés modulo height et width (ceux de la matrice, pas les paramètres), et toute la matrice destination est remplie en répétant la matrice other autant de fois que nécessaire. Matrix<T>& fillWith(unsigned int targetRow, unsigned int targetCol, const Matrix<U>& other, unsigned int fromRow = 0, unsigned int fromCol = 0, bool loop = false) Remplit la matrice (à partir de [targetRow][targetCol]) avec les données de la matrice other, depuis les coordonnées [fromRow][fromCol]. Si les coordonnées précisées font sortir de leur matrice et que loop est FAUX, seule la partie valide est concernée; si loop est VRAI, ces coordonnées sont réinterprétées modulo height et width, et toute la matrice destination est remplie en répétant la matrice other autant de fois que nécessaire. Matrix<T>& fillWith(unsigned int targetRow, unsigned int targetCol, const Matrix<U>& other, unsigned int fromRow, unsigned int fromCol, unsigned int height, unsigned int width, bool loop = false) Remplit la matrice (à partir de [targetRow][targetCol]) avec les données de la matrice other, depuis les coordonnées [fromRow][fromCol], et sur les longueurs height et width. Si la taille précisée fait sortir de la matrice et que loop est FAUX, seule la partie valide est concernée; si loop est VRAI, les coordonnées sont réinterprétées modulo height et width (de leur matrice), et toute la matrice destination est remplie en répétant la matrice other autant de fois que nécessaire. Matrix<T>& shift(int deltaheight, int deltawidth, const T& fill = T()) Décale les éléments de la matrice du nombre de lignes (deltaheight) et de colonnes (deltawidth) spécifiés (positifs ou négatifs). Cela laisse apparaître des cases qui seront remplies avec fill (0 par défaut pour les types de base). Voir aussi loop(). Matrix<T>& loop(int deltaheight, int deltawidth) Décale les éléments de la matrice du nombre de lignes (deltaheight) et de colonnes (deltawidth) spécifiés (positifs ou négatifs). Les éléments qui sortent de la matrice sont réintroduits du côté opposé. Voir aussi shift(). Matrix<T>& flip(bool bottomup = true, bool leftRight = true) Retourne la matrice; bottomup pour le sens haut-bas, leftRight pour le sens gauche-droite.
Matrix<T>& oppose(void) Change chaque valeur de la matrice en son opposée (par exemple, -1 donne 1 et vice-versa). Matrix<T>& inverse(void) Ce n'est pas une inversion de la matrice au sens de l'algèbre linéaire. Il s'agit simplement de calculer l'inverse (1/x) de chaque élément. Matrix<T>& sqr(void) Mise au carré de la matrice. Matrix<T>& sqrt(void) Ce n'est pas le calcul d'une racine de la matrice au sens de l'algèbre linéaire. Il s'agit simplement de calculer la racine de chaque élément. Matrix<T>& abs(void) Remplace chaque élément par sa valeur absolue. Cette dernière est implémentée par return (x<0) ? -x : x;. Elle ne peut donc être utilisée pour calculer le module d'un complexe. Matrix<T>& mulAdd(const Matrix<U>& m1, const Matrix<V>& m2) multiplie la matrice par m1+m2. Matrix<T>& pow(long n) Calcule la puissance n-ième par la formule de récurrence: x^0=1 ; x^1=x ; x^(2n) = (x^n)^2 ; x^(2n+1) = x.(x^(n))^2 Matrix<T>& pow(double y) Remplace chaque élément par sa puissance y. Cela utilise la fonction pow de <math.h>. Matrix<T> mulByVec(const Matrix<U>& lineMatrix) const Soit M une matrice et x un vecteur colonne. L'opération d'algèbre linéaire M*x produit un vecteur colonne y. mulbyvec émule cette opération, mais pour l'efficacité, le vecteur lineMatrix est donné en ligne, et le résultat également. Si la taille du vecteur ne correspond pas à la largeur de la matrice, ou si lineMatrix est une matrice quelconque, le code est prévu pour ne pas planter. Matrix<T>& writeToStream(ostream&) const Ecrit sur un flux les données nécessaires à la sauvegarde de la matrice (taille+éléments). Pour un affichage à l'écran, préférez operator<<(). Matrix<T>& readFromStream(istream&) Lit une matrice depuis un flux, telle qu'elle a pu être écrite par un appel à writeToStream(). Cette méthode est équivalente à operator>>(). T sum(void) const Calcule la somme des éléments de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T product(void) const Calcule le produit des éléments de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). pair<T,T> meanAndStandardDeviation(void) const Calcule en une passe moyenne et écart-type des éléments de la matrice. Si la matrice est vide, renvoie une paire d'objets de classe T construits par le constructeur par défaut (<0,0> pour les types de base). T mean(void) const Calcule la moyenne des éléments de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T standardDeviation(void) const Calcule l'écart-type des éléments de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T max(void) const Renvoie une copie de l'élément maximum de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T min(void) const Renvoie une copie de l'élément minimum de la matrice. Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T norm1(void) const Calcule la norme 1 de la matrice (somme des valeurs absolues des éléments). Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T norm2(void) const Calcule la norme 2 de la matrice (racine de la somme des carrés des éléments). Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). T norminf(void) const Calcule la norme infinie de la matrice (plus grande valeur absolue). Si la matrice est vide, renvoie l'objet de classe T construit par le constructeur par défaut (0 pour les types de base). La valeur absolue est implémentée par return (x<0) ? -x : x;. Elle ne peut donc être utilisée pour calculer le module d'un complexe. bool any(void) const Renvoie VRAI si au moins un des éléments de la matrice est évalué comme VRAI. Si la matrice est vide, renvoie FAUX. Cette méthode est équivalente à !none(). bool none(void) const Renvoie VRAI si aucun un des éléments de la matrice n'est évalué comme VRAI. Si la matrice est vide, renvoie VRAI. Cette méthode est équivalente à !any(). bool every(void) const Renvoie VRAI si tous les éléments de la matrice sont évalués comme VRAI. Si la matrice est vide, renvoie FAUX. T dotProduct(const Matrix<U>& other) const Renvoie le produit scalaire de la matrice avec other : somme des produits des éléments deux à deux. Si on fait un dotProduct d'une matrice avec elle-même, on obtient donc le carré de sa norm2(). Voir aussi la méthode statique dotProduct(). Méthodes statiquesstatic T DotProduct(const Matrix<T>& m1, const Matrix<T>& m2)Renvoie le produit scalaire de deux matrices : somme des produits des éléments deux à deux. Si on fait un DotProduct d'une matrice avec elle-même, on obtient donc le carré de sa norm2(). Voir aussi la méthode dotProduct(). static void FFT2D(Matrix<T>* Output_real, Matrix<T>* Output_imag, const Matrix<T>& Input_real, const Matrix<T>& Input_imag) Cette fonction effectue la Fast Fourier Transformation 2D (FFT2D) d'une matrice caractérisée par une partie réelle (Input_real) et une partie imaginaire (Input_imag). Le résultat est également scindé en une partie réelle (Output_real) et une partie imaginaire (Output_imag). On passe ainsi du domaine spatial au domaine fréquentiel. La FFT inverse est disponible via la fonction IFFT2D(...). Restrictions:
static void IFFT2D(Matrix<T>* Output_real, Matrix<T>* Output_imag, const Matrix<T>& Input_real, const Matrix<T>& Input_imag) Cette fonction effectue la Fast Fourier Transformation 2D inverse (IFFT2D) d'une matrice caractérisée par une partie réelle (Input_real) et une partie imaginaire (Input_imag). Le résultat est également scindé en une partie réelle (Output_real) et une partie imaginaire (Output_imag). On passe ainsi du domaine fréquentiel au domaine spatial. La FFT directe est disponible via la fonction FFT2D(...). Restrictions:
static void FFT2D(Matrix<T>* Output_real, Matrix<T>* Output_imag, const Matrix<T>& Input_real, const Matrix<T>& Input_imag, const FFTSetup& fftSetup) [Apple Only] Cette fonction se comporte comme FFT2D(...). Elle est disponible sous MacOS X pour profiter pleinement des optimisations possibles de la FFT du système si l'on en exécute plusieurs d'affilée. La FFT2D du système est documentée dans le vDSP.pdf accompagnant le framework vecLib. static void IFFT2D(Matrix<T>* Output_real, Matrix<T>* Output_imag, const Matrix<T>& Input_real, const Matrix<T>& Input_imag, const FFTSetup& fftSetup) [Apple Only] Cette fonction se comporte comme IFFT2D(...). Elle est disponible sous MacOS X pour profiter pleinement des optimisations possibles de la FFT du système si l'on en exécute plusieurs d'affilée. La FFT2D du système est documentée dans le vDSP.pdf accompagnant le framework vecLib. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||